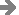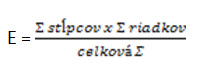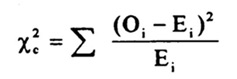Step: Najprv určime závislú a nezávislú premennú....
|
| |
Najprv určime závislú a nezávislú premennú. |
|
|
|
Nezávislá: pohlavie
Závislá: výskyt problémového správania |
|
Step: Potom naformulujme hypotézy H0 a H1. ...
|
| |
Potom naformulujme hypotézy H0 a H1. |
|
|
|
H0: Neexistuje štatisticky signifikantná súvislosť medi pohlavím a výskytom problémového správania. Alebo: Problémové správanie sa u chlapcov a dievčat vo výskumnej vzorke vyskytuje rovnako.
H1: Existuje štatisticky signifikantná súvislosť medi pohlavím a výskytom problémového správania. Alebo: Problémové správanie sa u chlapcov a dievčat vo výskumnej vzorke nevyskytuje rovnako. Alebo: Existujú štatisticky významné rozdiely medzi výskytom problémového správania u chlapcov a u dievčat. |
|
Step: Zostavíme si kontingenčné tabuľky pre pozorované (O) a očak...
|
| |
Zostavíme si kontingenčné tabuľky pre pozorované (O) a očakávané (E) početnosti |
|
|
|
Tabuľku pre pozorované početnosti už máme. Pri výpočte očakávaných početností pre každý riadok a stĺpec tabuľky (pre každú bunku) postupujeme podľa vzorca:
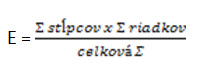
Očakávané početnosti sú teda nasledovné: 40,97, 76,02, 42,03 a 77,97
|
|
Step: Ďalej vypočítame hodnotu Chí-kvadrátu podľa vzorca: ...
|
| |
Ďalej vypočítame hodnotu Chí-kvadrátu podľa vzorca: |
|
|
|
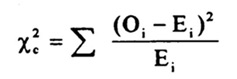
= 1,87 |
|
Step: Určíme počet stupňov voľnosti dF...
|
| |
Určíme počet stupňov voľnosti dF |
|
|
|
Podľa vzťahu: dF= (počet stĺpcov – 1) x (počet riadkov – 1)
Tj. dF=1 |
|
Step: Určíme tabuľkovú hodnotu pre príslušný Chí-kvadrát na počte...
|
| |
Určíme tabuľkovú hodnotu pre príslušný Chí-kvadrát na počte stupnov voľnosti (tabuľky nájdete na internete alebo v linku na konci kapitoly) |
|
|
|
Tabuľková hodnota Chí-kvadrátu (na hladine 0,05) = 3,84 |
|
|
| |
Rozhodnutie |
|
|
|
Keďže je tabuľková hodnota Chí-kvadrátu (3,84) váčšia ako vypočítaná hodnota (1,87) konštatujeme že nemáme dostatočné dôkazy na to, aby sme H0 zamietli. Tvrdíme teda že v našej výskumnej vzorke medzi premennými pohlavie a výskyt problémového správania nie je vzťah.
(ak by vypočítaná hodnota bola váčšia ako 3,84 tvrdili by sme opak a prijali tým pádom H1) |
|